/natureduca/fisica-fuerzas-y-equilibrio-sistemas-de-fuerzas-02

---

1 2 3

Composición de fuerzas paralelas y de igual sentido

l tratarse de fuerzas de igual dirección y sentido, el módulo o magnitud de la resultante será igual a la suma de los módulos de las fuerzas que se componen, y la dirección y el sentido serán los mismos que el de ellas. El problema estriba entonces en determinar el punto de aplicación O, de la resultante.

En el caso de que el sistema esté formado por dos fuerzas, puede demostrarse que la resultante está aplicada en un punto intermedio situado en la línea que une los puntos de aplicación O1 y O2 de las fuerzas que se suman, y a distancias de ellos que son inversamente proporcionales a sus magnitudes respectivas:

La resultante estará, por tanto, más cerca de la fuerza de mayor módulo.

La determinación del punto de aplicación O puede realizarse bien por un procedimiento algebraico, o bien por un procedimiento gráfico. El procedimiento algebraico supone resolver el sistema de ecuaciones:

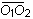en donde F1 , F2 y la distancia entre ellas son conocidos. Cualquiera de las distancias u fijará la posición del punto O de aplicación de la resultante R.

El procedimiento gráfico, una vez representado el sistema, se desarrolla a través de los siguientes pasos:

a) En O1 se representa una fuerza de igual magnitud y sentido a F2.

b) En O2 se representa una fuerza de igual magnitud y sentido contrario a F1.

c) Se unen sus extremos mediante una línea recta que corta el segmento 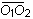en un punto O que es precisamente el punto de aplicación de la resultante R.

La aplicación de ambos procedimientos puede extenderse al caso de un sistema formado por más de dos fuerzas, componiéndolas dos a dos. La resultante, siempre que se trate de fuerzas paralelas y de igual sentido, será no nula.

Cuando dos fuerzas actúan en la misma dirección y sentido, la resultante tiene la misma dirección y sentido que ellas, y su módulo es la suma de los módulos de los componentes.

1 2 3

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios